我的算法书 - 网络流总述

网络流

引用:一个题目

如下图,可以想像成一个输水网络, $S$ 是起点, $T$ 是终点.每一条边上有两个值 $(x,y)$ , $x$ 表示这条边现在的流量, $y$ 表示这条边的最大流量. $T$ 结点现在接收的流量为 $4$ .

问: $T$ 结点能接收的最大流量为多少?

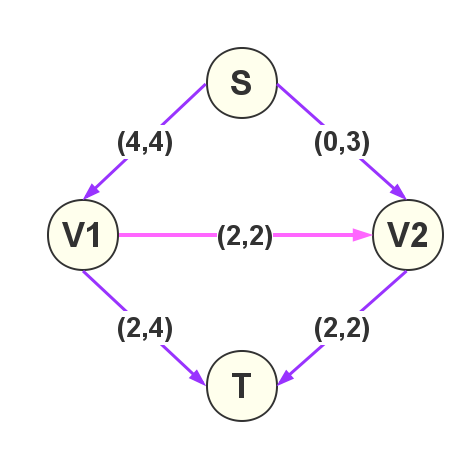
如下图所示,最大为 $6$ !

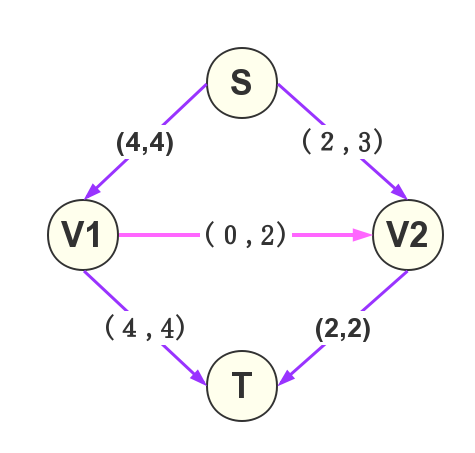
定义：什么是网络流

网络: 网络是一个有向带权图，包含一个源点和一个汇点，没有反平行边。

digraph hello {
    rankdir=LR;
    a->b[minlen=3];
    b->a[headlabel="反平行边",labeldistance=5,labelangle=8,style="dashed"];
}

网络流 :网络流即网络上的流，是定义在网络边集 $E$ 上的一个非负函数 $fow=\{fow (u,v)\}$ ， $flow(u,v)$ 是边上的流量。

可行流 :满足以下两个性质的网络流flow称为可行流。

2.网络流中的约束条件

网络流中的常用名词

$V$ 表示整个图中的所有结点的集合.
$E$ 表示整个图中所有边的集合.
$G = (V,E)$ ,表示整个图.
$s$ 表示网络的源点, $t$ 表示网络的汇点.
对于每条边 $(u,v)$ ,有一个容量 $c(u,v) (c(u,v)>=0)$
如果 $c(u,v)=0$ ，则表示 $(u,v)$ 不存在于网络中。
如果原网络中不存在边 $(u,v)$ ，则令 $c(u,v)=0$
对于每条边 $(u,v)$ ,有一个流量 $f(u,v)$ .

3.网络流的三个限制限制条件

一个网络流必须满足下面的条件

1、容量限制: $f(u,v)<=c(u,v)$
2、反对称性: $f(u,v) = - f(v,u)$
3、流量平衡: 对于不是源点也不是汇点的任意结点,流入该结点的流量和等于流出该结点的流量和。

结合反对称性,流量平衡也可以写成:

\sum_{u\epsilon V} f(v,u)=0

只要满足这三个性质,就是一个合法的网络流,也称为可行流。

弧的分类

若给定一个可行流 $F=(F_{ij})$ ,我们把网络中 $F_{ij}=C_{ij}$ 的弧称作饱和弧， $F_{ij}<C_{ij}$ 的弧称作非饱和弧， $F_{ij}=0$ 的弧称作零流弧, $F_{ij}>0$ 的弧称作非零流弧

若 $P$ 是网络中联结源点 $s$ 和汇点 $t$ 的的一条路(不用管边的有向性)，我们定义路的方向是从 $s$ 到 $t$ ，则路上的弧被分为两类：一类与路的方向一致，称为前向弧；另一类和路的方向相反，称为后向弧

知识点思维导图

digraph G {

    ranksep=0.74;
    node[shape="box"];
    "网络"->"网络流";
    edge[samehead=h1,sametail=t1,headport=n,tailport=s];
    "网络流"->"满足的性质"->{"容量约束":s,"流量守恒"}->"网络最大流"[tailport=same];
    "网络流"->"相关名词"->{"源点:s","汇点:t"};
    "网络最大流"->"增广路算法"[label="解决思路"];
    subgraph a1 {
        rankdir=LR;
        "增广路算法"->"相关概念"->{"实流网络","残余网络","可增广路","可增广量",t1}->t2;
    }
    t1[label="残余网络上的增广路的增流,减流操作",shape=plain];
    t2[label="增广路算法:Ford-Fullkerson"]
    t3[label="不是一种具体的算法,而是一种思路",shape=plain]

    {
        rank=same;
        t2,t3;
    }

    t5[label="随意找增广路:可能有很高的复杂度",shape=plain]
    t2->t5->{"最短路径优先","最大容量优先"};

    t4[label="SAP"];
    "最短路径优先"->t4[headlabel="最短增广路算法",labeldistance=6,labelangle=60];
    "最短路径优先"->"朴素Dinic"[label="最短增广路算法"];
    t4->"ISAP"[label="优化"];
    "ISAP"->"gap优化"[label="优化"];
    "朴素Dinic" ->"多路增广Dinic"[label="优化"];
    "多路增广Dinic" -> "当前弧优化"[label="优化"];
}

经典的网络流24题

问题编号	题目地址	问题名称	问题模型	转化模型
1	loj6000	飞行员配对方案问题	二分图最大匹配	网络最大流
2	loj6001	太空飞行计划问题	最大权闭合图	网络最小割
3	loj6002	最小路径覆盖问题	有向无环图最小路径覆盖	网络最大流
4	loj6003	魔术球问题	有向无环图最小路径覆盖	网络最大流
5	loj6004	圆桌问题	二分图多重匹配	网络最大流
6	loj6005	最长递增子序列问题	最多不相交路径	网络最大流
7	loj6006	试题库问题	二分图多重匹配	网络最大流
8		机器人路径规划问题	(未解决),具说不是网络流	最小费用最大流
9	loj6007	方格取数问题	二分图点权最大独立集	网络最小割
10	loj6008	餐巾计划问题	线性规划网络优化	最小费用最大流
11	loj6009	航空路线问题	最长不相交路径	最小费用最大流
12	loj6010	软件补丁问题	最小转移代价	最短路径
13	loj6011	星际转移问题	网络判定	网络最大流
14	loj6012	孤岛营救问题	分层图最短路径	最短路径
15	loj6013	汽车加油行驶问题	分层图最短路径	最短路径
16	loj6014	数字梯形问题	最大权不相交路径	最小费用最大流
17	loj6015	运输问题	网络费用流量	最小费用最大流
18	loj6121	分配问题	二分图最佳匹配	最小费用最大流
19	loj6122	负载平衡问题	最小代价供求	最小费用最大流
20	loj6223	深海机器人问题	线性规划网络优化	最小费用最大流
21	loj6224	最长k可重区间集问题	最大权不相交路径	最小费用最大流
22	loj6225	最长k可重线段集问题	最大权不相交路径	最小费用最大流
23	loj6226	火星探险问题	线性规划网络优化	最小费用最大流
24	loj6227	骑士共存问题	二分图最大独立集	网络最小割

费用流

洛谷 P2488 [SDOI2011]工作安排
洛谷 P2050 [NOI2012]美食节
洛谷 [SCOI2007]修车

引用/参考

结论：学Dinic 代码量少,容易记忆！

目录